发布时间:2025-01-20 10: 00: 00
品牌型号:联想GeekPro 2020
系统:Windows10 64位专业版
软件版本:Maple 2024
在工程设计和数据分析中,大家经常用Maple来算特征方程,这样可以快速看出矩阵的结构,预测系统的变化趋势。而特征值还能帮我们更深入地了解矩阵的稳定性,对优化模型结构特别有用。有关Maple软件怎么求特征方程,Maple软件怎么求特征值的问题,本文将进行详细介绍。
特征方程体现了矩阵系统的特点,是分析矩阵稳定性和动态表现的关键工具。比如,在机械制造、网络设计和数据分析中,特征方程常用来研究系统的振动模式、电路特性以及数据变化趋势,为解决复杂问题提供了很大帮助。

1、特征方程是描述矩阵性质的一个多项式方程,其形式为det(A−λI)=0。其中,λ是特征值,I是单位矩阵。打开Maple数学软件,新建一个工作表,输入“with(LinearAlgebra)”加载线性代数库,用于支持矩阵运算。

2、输入“A:=Matrix([[2,1,3],[4,-2,1],[1,5,2]])”,使用Matrix([...])命令创建一个3×3的矩阵A。

3、输入“P:=CharacteristicPolynomial(A,lambda)”,使用CharacteristicPolynomial命令,求矩阵A的特征多项式。

4、在机械工程中,刚度矩阵的特征方程能反映系统的振动频率。假设一个三质量点的弹簧质量系统,其刚度矩阵为K,我们要求出K的特征方程。加载线性代数库后,输入“K:=Matrix([[10,-5,0],[-5,15,-10],[0,-10,10]])”,定义刚度矩阵K。

5、输入“P:=CharacteristicPolynomial(K,lambda)”,求出矩阵K的多项式方程,输出结果为λ^3-35*λ^2+275*λ-250。

特征值是特征方程的解,通常用来描述矩阵的变化特性。在实际应用中,研究人员经常用Maple软件来求特征值,用于分析矩阵系统的稳定性,模拟物理系统的运行。
1、加载线性代数库后,使用Matrix函数定义3×3的矩阵A。

2、输入eigenvalues:=evalf(Eigenvalues(A)),计算矩阵A的特征值,并把结果转换成数值形式。在Maple里,evalf是用来把结果变成数值的,Eigenvalues是用来算矩阵特征值的命令。

3、输入real_eigenvalues:=map(Re,eigenvalues),用map命令提取变量eigenvalues的实部Re,并把结果存到变量real_eigenvalues中。运行后Maple会返回矩阵A的特征值,分别是λ1=5.8944,λ2=−1.9472,λ3=−1.9472。

4、在电路网络中,导纳矩阵的特征值反映了系统的阻抗特性和稳定性。假设一个三节点电路的导纳矩阵为Y,求矩阵Y的特征值。

5、输入“eigenvalues:=Eigenvalues(Y)”,利用Eigenvalues函数求解矩阵特征值。

6、使用evalf命令,将特征值转换成数值形式。

7、提取特征值的实数部分,Maple返回导纳矩阵的特征值为λ1=8.6143、λ2=0.9119、λ3=5.4738。

以上便是Maple软件怎么求特征方程,Maple软件怎么求特征值的全部内容。学会求特征方程和特征值,可以更好地分析矩阵的性质,还能研究系统的动态表现和稳定性。用Maple软件算特征方程和特征值,不但能帮我们降维数据,还能显著提高计算效率。更多数学技巧,可以在安装Maple数学工具后进行体验。
作者:MuseFrog
展开阅读全文
︾
读者也喜欢这些内容:

Maple导入数据画三维曲面图 怎么对Maple作出的图形进行编辑
Maple除具备强大的数据处理、符号运算等功能外,还具备强大的数据可视化功能,我们可以通过这一功能绘制统计图,函数图,曲面图等各种图形,大大便利了讲授、教学和研究工作。如何使用Maple导入数据画三维曲面图,怎么对Maple作出的图形进行编辑。本文就上述两个问题,向大家作简单介绍。...
阅读全文 >

Maple怎么计算解方程组 Maple如何显示计算过程
Maple作为一款专业的数学软件,为我们的数学分析以及科研工作提供了不少便利。我们在使用Maple的过程中,经常会遇到求解计算方程组以及显示计算过程的情况。接下来给大家介绍Maple怎么计算解方程组,Maple如何显示计算过程的具体内容。...
阅读全文 >
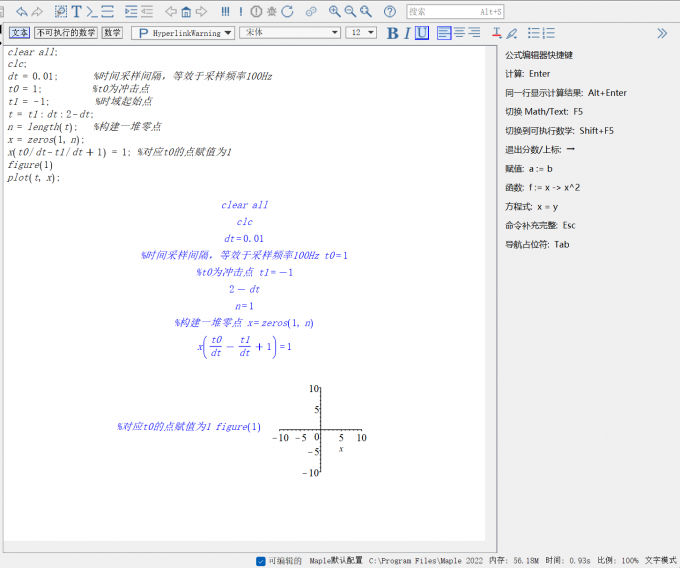
Maple怎么画单位冲激函数 Maple怎么画两个三维图
相信对于许多学生党以及科研党来说,进行数学分析计算也是大家在学习当中的一项重要任务。而在数学分析计算的过程中,同样也少不了一款好用的数学公式计算软件,这里给大家介绍一款名为Maple的数学公式计算软件,同时为大家讲解一下Maple怎么画单位冲激函数,Maple如何走义方程的具体内容。...
阅读全文 >

Maple如何计算矩阵的行列式 Maple如何计算行列式
作为矩阵的基本特性之一,行列式常被用来判断线性方程组解的存在性,帮助研究人员深入了解矩阵的几何性质。使用Maple数学软件,可以快速计算矩阵的行列式,让我们直观地了解空间变化的缩放比例和方向性。有关Maple如何计算矩阵的行列式,Maple如何计算行列式的问题,本文将进行详细介绍。...
阅读全文 >